The World of Derivatives
by Kennedy Coverdale & Liza Cohen

Let's use the Power Rule!

The power rule is only applied to power functions, or functions with a variable base and a numerical exponent.
When solving for a derivative using the power rule, you are simply taking the power that the function is raised by and multiplying it to the leading coefficient that is attached to a variable. Then subtracting 1 from the original power given. If there is no variable attached to the coefficient, it is just a constant number and can be eliminated.This is because if you were to graph a constant, the line would be straight and there would be no slope. Therefore, it wouldn’t affect the function because there would be no rate of change.
Let's look at some short example problems to start off.
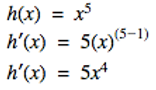
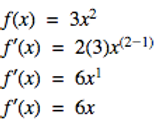
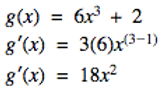
Let's apply the power rule to the real world!
Here's a scenario in which the power rule and derivatives can be applied.
Problem:
The flight attendants at U.S. Airways need to inform their passengers when the plane is ready for liftoff. The particular plane they are traveling on is called “Airbus a319”. The plane flies at a rate of 541 miles per hour (MPH Club) - about 241.84 meters per second. If the plane starts to move at a rate of 0 m/s and the flight attendants are aware that it takes 30 seconds for the plane to reach full speed at 241 m/s, how fast is the plane accelerating by? How long does the runway need to be?
Solution:
To find the acceleration in which the plane is moving at, we had to use the position formula that is usually referred to in physics. With this formula, we can plug in the information we already know and apply the power rule.
In words, the formula below is solving for position which is what is represented by “x”. The position equals 1/2 multiplied by acceleration (“a”) multiplied by time squared (“t”) plus the initial velocity (“v”) multiplied by time plus the initial position. Since we are solving for the acceleration first, we can plug in numbers for the variables that we already know of. But before we do that, we have to find the derivative by using the power rule.
Since we are solving for the acceleration first, we can plug in numbers for the variables that we already know of. But before we do that, we have to find the derivative by using the power rule.
The derivative of the position which is “x” is represented by
Before even applying the derivative, we can simplify our equation by plugging in numbers we already know/canceling variables. In other words, v0 represents the starting velocity. In the problem given, we know that the plane starts to move at a rate of 0 meters per second. We also know that x0 represents the starting position. We also know the starting position is 0 since the plane isn’t moving or changing position.
Therefore:
We can consider these numbers invisible because in the end, they still won’t affect our answer. So, we can just take the derivative of the function given by multiplying the power raised from the variable it is attached to by the leading coefficient.

We know it takes 30 seconds for the plane to take off so we substituted “t” for 30 seconds.
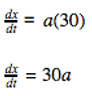
We know the position of the plane has to reach 241 meters per second so we substituted for 241 and solved for “a” - the acceleration by using simple algebra to isolate the variable.

The plane is accelerating at a speed of 8.03 meters per second per second.
To find how long the runway needs to be, we need to plug in the plane’s acceleration to find its position into our original equation by using simple algebra. In other words, we used the power rule to find the derivative (the acceleration) of our original given formula. Now that we know the acceleration, we can solve for the plane’s position.
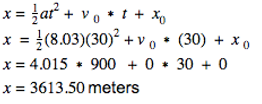
This means that the plane’s runway will have to be 3613.50 meters for it to take off 30 seconds later at a rate of 241 meters per second.