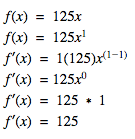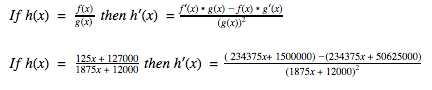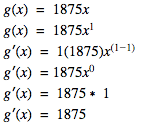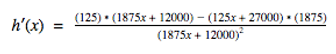The World of Derivatives
by Kennedy Coverdale & Liza Cohen
Let's use the Quotient Rule!


Similar to the objective of the product rule, you can use the quotient rule to find the derivative of a function that is being divided by another function. To apply the quotient rule, you would use almost the same process that you would use when applying the product rule. You’d take the derivative of your first function, multiply it by the original second function, then subtract that from the original first function, multiplied by the derivative of the second. That entire answer, would be divided by the original second function squared.
Let's look at some short example problems to start off.

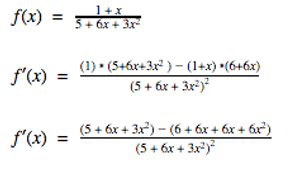
Let's apply the quotient rule to the real world!
Here's a scenario in which the quotient rule and derivatives can be applied.
Problem:
Hannah is interested in applying to her local Dunkin Donuts to save up for college. She did some research and found out that there was 127,000 cashiers working in 2011 and 127,500 cashiers working in 2015 (Dunkin Donuts Cooperation Customer Service). The cashiers got paid an average of $12,000 (Glassdoor) in 2011 and $19,500 (Job Applications) in 2015. The more experience you have at Dunkin Donuts, the more your pay increases. Hannah wants to find out how much her annual salary would be increasing by. She also wants to know how the rate in which her salary is changing at in 2016.
Solution:
The first thing we did to approach this problem is organize our information. We created coordinate points so we could make equations. These equations represent the change of employees over time and the change in their salaries, from 2011 to 2015.
cashier employees: (0,127,000) to (4,127,500)
127,500 - 127,000 = 500
500/4 = 125
125 represents the rate in which the employees are increasing by over the time period of 4 years and our y-intercept is the amount of employees that they started with in 2011.
f(x) = 125x + 127,000
We did the same process for the amount of salary the cashiers are earning.
salary earned: (0,12,000) to (4,19,500)
19,500 - 12,000 = 7500
7500/4 = 1875
1875 represents the rate in which the salary for the employees is increasing over the time period of 4 years and our y-intercept is the amount of money the employees started out with in 2011.
g(x) = 1875x + 12,000
Now that we have our two equations, we can divide the amount of cashiers by the salary they are earning to find out how much Hannah’s salary would be increasing by.
Therefore we referred to the standard formula for using the quotient rule.
We applied the quotient rule by finding the derivative of f(x) multiplied by the original function of g(x) subtracted by the original function of f(x) multiplied by the derivative of g(x), all divided by g(x) squared. By finding the derivative, we applied the power rule to each function to find the derivative but used the formula for the quotient rule as our process. Here’s how we got the derivative of each separate function:
If f(x) = 125x + 127000 then f'(x) = 125
We dropped our constant number then found the derivative of 125x.
If g(x) = 1875x + 12000 then g'(x) = 1875
We dropped our constant number then found the derivative of 1875x.
Once we knew the derivative of f(x) and g(x), the derivative of the entire function using the quotient rule is:
Then, we simplified by distributing 125 to 1875x + 12000 and 1875 to 125x + 27000.
Then, we used this equation to plug in 5 everytime we see “x”. This is because Hannah wants to find out the rate in which her salary would be changing in 2016, which is 5 years after 2011.
This means that in 2016, her salary would be decreasing by -.1075202626. Her salary would be decreasing at this rate instead of increasing because over time, the amount of employees at Dunkin Donuts is increasing. Therefore, the more employees that are working at Dunkin Donuts, the less money there is to be distributed to every employee.