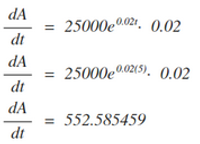Let's apply the chain rule to the real world!

 

Here's a scenario in which the chain rule and derivatives can be applied. 

 

Problem:

 

A pair of parents place $25,000 into the bank in order to save up for a new car. At the bank, the teller lets them know that their account will earn 0.02% interest a year (“Bank Account Interest Rates”, Bank of America). First, write an equation modeling how the account’s balance is changing as a function of t, representing the amount of years. Then, using said equation, find the amount of money the account will have after five years. Then, using the knowledge of derivatives, find the rate of change of the amount of the money after five years.

 

Solution: 

 

First, given the situation, we know to use the equation                 We know that P = 25000 since that’s the initial amount that was placed into the bank, and that r = 0.02 since the rate at which the account is changing is 0.02%. Using this information, we can now construct the equation.

 

 

 

Now we need to find the amount of money that will be in the account after 5 years. Since t=5, we can substitute t for 5, and use basic algebra to solve for "a".

 

 

 

 

 

 

This means that there will be approximately 27,629.27 dollars in the bank after 5 years.

 

Now, we can use our knowledge of derivatives in order to find the change of the amount of money in the account after five years. First, using the rules, we have to find the derivative equation. Looking at the original function, we can tell that the outside function is 25000ef(x), and the inside function is 0.02t. Using the chain rule, we find that the derivative function is:

 

 

 

Now that we have the derivative equation, we can plug in 5 for t in order to find the change in the amount of money in the account after 5 years.

 

 

 

 

 

 

 

 

This means that after five years, the money in the account is changing by approximately $552.59 dollars per year.