The World of Derivatives
by Kennedy Coverdale & Liza Cohen


Let's use the Exponential Rule!
Exponential functions are functions with a constant base and variable exponent. They differ from power functions because instead of the variable being in the base, it’s in the exponent. Concerning the derivatives of exponential functions, there are set rules as to how to differentiate said functions, depending on what kind of exponential function you run into.
Let's look at a short example problem to start off.
Let's apply the exponential rule to the real world!
Here's a scenario in which the exponential rule and derivatives can be applied.
Problem:
Based on the data from Peak Bagger (Peak Bagger), the exponential model to predict the population in Boston, Massachusetts after the year 2010 is
This is where "x" represents the amount of years since 2010 and y represents the population of Boston after 2010. Use this model to find the population of Boston in the year 2040. Then find and use the derivative of the function of the population of Boston to predict how fast the population of Boston will be changing in the year 2040.
Solution:
First, using the equation given in the problem, we can find the population of Boston in the year 2040. To do this, we notice that the variable x represents the amount of years since 2010. Since 2040 is thirty years after 2010, we replace the "x" with 30. Then, we use simple algebra in order to find the population.

This means that the population of Boston in the year 2040 is approximately 5,171,051 people.
Using our knowledge of derivatives, it’s simple to find the derivative equation of the original function.
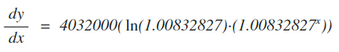
After finding the derivative equation, we can now predict the change of the population in the year 2040. Because 2040 is thirty years after 2010, we have to replace the "x" in the derivative equation with 30. Then, using simple algebra, solve for "y".

This means that in the year 2040, the population will be changing by 42,887 people.