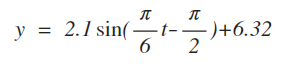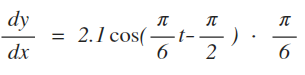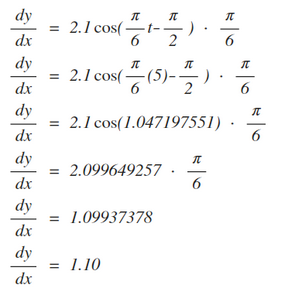The World of Derivatives
by Kennedy Coverdale & Liza Cohen

Let's use the Trigonometric Rule!

Trigonometric functions are functions with a trigonometric value, like cosine or sine. The function usually involves taking the sine, cosine, tangent, etc. of a value or a another function. Concerning derivatives of said functions, there are set rules as to how to differentiate the functions. Most of the time though, when taking the derivative of a trigonometric function, we have to use the chain rule since the function is taking the trigonometric value of another function, not just "x".
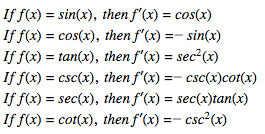
Let's look at a short example problem to start off.
Let's apply the trigonometric rule to the real world!
Here's a scenario in which the trigonometric rule and derivatives can be applied.
Problem:
Based on the data from Time and Date (Time and Date), the monthly sunset times in Boston, Massachusetts can be modeled by the function where t equals the months after January (meaning since January is the first month, “t” would equal 0, and February would be t=1, etc.), and “y” equals the sunset time at the beginning of the month. Based on your knowledge of trigonometric functions, find the sunset time in June, and using your knowledge of derivatives, find how much the sunset time is changing in June.
Solution:
Using the given equation, we can find the sunset time in June. Since “t” is the number of months after January, since June is the sixth month, it’s five months after January, meaning t=5. We can plug that into the original equation and find our answer using simple algebra.
After finding the y, we need to convert it into minutes. By multiplying 0.36 by 60 since there are 60 seconds in a minute, we get 6:21 as our sunset time in June.
Now that we found the first part of the problem, we can use our knowledge to find the derivative function of the original function.
First, we can drop the 6.32 since it’s a constant. We can also keep the 2.1, practically ignoring it since it’s a constant multiple of the sine function. Focusing on the sine function, we see that this involves two rules: the chain rule and one of the trigonometric rules. First, using the chain rule, we know we need to evaluate the original inside function with the derivative of the outside function. The inside function is which means that the derivative is The outside function is f(x)=sin(g(x)), meaning the derivative of the outside is f'(x)=cos(g(x)). Using this information, we can easily put the equation together.
Now that we’ve found the derivative equation, we can plug in 5 for t in order to find the rate at which the sunset time is changing in the month of June.
After converting the answer to hour:minute format, the final answer is that the sunset time is changing by 1 minute and 6 seconds during the month of June.